Challenge
The idea is to fill a 9×9 grid with digits so that each column, each row, and each of the nine 3×3 sub-grids that compose the grid (also called “boxes”) contains all of the digits from 1 to 9.
The person who created the puzzle provides a partial solution so that some squares already have numbers. Typically, there are enough initial numbers to guarantee a unique solution.
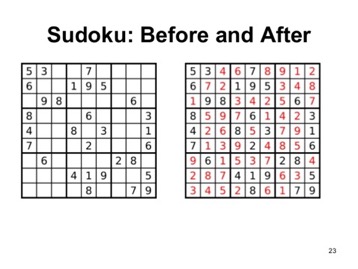
Something that starts like this will be solved and turned into this:
We’ll use the traditional board layout/style. A puzzle is made up of:
Rules
a spot holds a single number 1-9
a square is a 3x3 group of spots
a board is made up of a 3x3 group of squares
a row spans nine squares in a straight line left-to-right across the board
a column spans nine squares in a straight line top-to-bottom across the board
at the start of a Sudoku game, one or more spots are blank
A valid solution is made up of:
each square has each number 1-9
each row has each number 1-9
each column has each number 1-9
each square, column, and row must have the numbers 1-9 in them and cannot have duplicates
How I solved it
The main block of code will iterate over all 81 square and calculate a uniqueness factor for each square:
def get_uniqueness_board(board)
turn_array = []
(0..80).each do |box_number|
if return_box(box_number, board) == 0
turn_array << [uniqueness(box_number, board), box_number]
end
end
turn_array
endIf a square has a uniqueness of 8, implying that the square has only one remaining possible value, it will substitute in that value. If a square can be solved using an intersection method, it will also be substituted.
def solve!(board)
run_array = []
change_count = 0
(0..80).each do |box_number|
if return_box(box_number, board) == 0
turn_array = uniqueness(box_number, board)
if turn_array.length == 8
only_possibility = possible_values(turn_array)[0]
edit_board(box_number, only_possibility, board)
change_count += 1
elsif intersection?(box_number, turn_array, board)
change_count += 1
end
end
end
return change_count
endIf after an iteration of the board, the change count is zero, the program will make a guess on a square with the highest uniqueness and recursively try to solve the board using the main solve block.
def recursive_method(board, recursion_count = 0, solve_count = 1)
if solved?(board)
# binding.pry
@solved_board = board
return board
elsif !(maximum_length(board) == 9)
while solve_count > 0
solve_count = solve!(board)
end
if solved?(board)
return board
end
turn_array = get_uniqueness_board(board)
sorted_array = turn_array.sort {|array1, array2| array2[0].length <=> array1[0].length}
max_length = sorted_array[0][0].length
if max_length < 9
selected_arrays = sorted_array.select {|array| array[0].length == max_length}
possible_values(selected_arrays[0][0]).each do |possible_value|
temp_board = Marshal.load(Marshal.dump(board))
edit_board(selected_arrays[0][1], possible_value, temp_board)
if recursive_method(temp_board, recursion_count += 1) != nil
return recursive_method(temp_board, recursion_count += 1)
end
end
end
end
nil
end